機率論的相關重要定理

機率公理[編輯]

主條目：機率公理

如果一個函數${\displaystyle P:S\to \mathbb {R} ,\ A\mapsto P(A)}$指定給每一個事件空間 ${\displaystyle S}$ 中的事件 ${\displaystyle A}$ 一個實數 ${\displaystyle P(A)}$，並且其滿足下面的 3 個公理，那麼函數 ${\displaystyle P}$ 叫做機率函數，相應的 ${\displaystyle P(A)}$ 叫做事件 ${\displaystyle A}$ 的機率。

公理 1： ${\displaystyle 0\leq P(A)\leq 1\ (A\in S)}$ 事件 ${\displaystyle A}$ 的機率 ${\displaystyle P(A)}$ 是一個0與1之間（包含0與1）的非負實數。

公理 2： ${\displaystyle P(S)=1}$ 事件空間的機率值為 1 。

公理 3： ${\displaystyle P(A\cup B)=P(A)+P(B)}$，如果 ${\displaystyle A\cap B=\varnothing }$ 互斥事件的加法法則。這裡需注意：公理3可以推廣到可數個互斥事件的聯集。

機率的計算[編輯]

需要提及的是下面將要介紹的 9 個計算機率的定理與上面已經提及的事件的計算沒有關係，所有關於機率的定理均由機率的 3 個公理得來，同時適用於包括拉普拉斯機率和統計機率在內的所有機率理論。

定理 1 (互補法則)[編輯]

與 ${\displaystyle A}$ 互補事件的機率始終是

${\displaystyle P({\bar {A}})=1-P(A),\in S}$

證明：
事件 ${\displaystyle A}$ 和 ${\displaystyle {\overline {A}}}$ 是互補關係，由公理 3 和公理 2 可得

${\displaystyle P(A)+P({\bar {A}})=P(S)=1}$

${\displaystyle \Rightarrow P({\bar {A}})=1-P(A)}$

利用互補法則，可以解決下面這個問題，在兩次連續旋轉的輪盤遊戲中，至少有一次是紅色的機率是多少？
第一次旋轉紅色不出現的機率是 19/37 ，按照乘法法則，第二次也不出現紅色的機率是 (19/37)² = 0.2637，因此在這裡互補機率就是指在兩次連續旋轉中至少有一次是紅色的機率，
${\displaystyle P=1-\left({\frac {19}{37}}\right)^{2}=0.7363}$

定理 2[編輯]

不可能事件的機率為零：

${\displaystyle P(\varnothing )=0}$

證明：

${\displaystyle \varnothing }$ 和 ${\displaystyle S}$ 是互補事件，按照公理 2 有

${\displaystyle P(S)=1}$，再根據上面的定理 1 得到

${\displaystyle P(\varnothing )=1-1=0}$

定理 3[編輯]

如果若干事件 ${\displaystyle A_{1},A_{2},\cdots A_{n}\in S}$ 每兩兩之間是空集關係，那麼這些所有事件集合的機率等於單個事件的機率的和。

${\displaystyle P(A_{1}\cup \cdots \cup A_{n})=\sum _{j=1}^{n}P(A_{j})}$

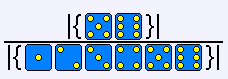
注意針對這一定理有效性的決定因素是 ${\displaystyle A_{1}\cdots A_{n}}$ 事件不能同時發生。例如，在一次擲骰子中，得到 5 點或者 6 點的機率是：

${\displaystyle P=P(A_{5})+P(A_{6})=}$ ${\displaystyle ={\frac {2}{6}}={\frac {1}{3}}}$

定理 4[編輯]

如果事件 ${\displaystyle A}$，${\displaystyle B}$ 是差集關係，則有，

${\displaystyle P(A\setminus B)=P(A)-P(A\cap B)}$

證明：

事件 ${\displaystyle A}$ 由下面兩個事件組成：

${\displaystyle A\setminus B}$ 和 ${\displaystyle A\cap B}$
由公理 3 得，

${\displaystyle P(A)=P(A\setminus B)+P(A\cap B)}$

定理 5 (任意事件加法法則)[編輯]

對於事件空間 ${\displaystyle S}$ 中的任意兩個事件 ${\displaystyle A}$ 和 ${\displaystyle B}$，有如下定理：

${\displaystyle P(A\cup B)=P(A)+P(B)-P(A\cap B)}$

證明：

事件 ${\displaystyle A\cup B}$ 由下面三個事件組成：
${\displaystyle A\cup B=(A\setminus B)\cup (A\cap B)\cup (B\setminus A)}$
首先根據定理 4 有：
${\displaystyle {\begin{array}{lcr}P(A\setminus B)&=&P(A)-P(A\cap B)\\P(B\setminus A)&=&P(B)-P(A\cap B)\end{array}}}$

再根據定理 3 得：

${\displaystyle {\begin{aligned}P(A\cup B)&=P(A\setminus B)+P(A\cap B)+P(B\setminus A)\\&=P(A)-P(A\cap B)+P(A\cap B)+P(B)-P(A\cap B)\\&=P(A)+P(B)-P(A\cap B)\end{aligned}}}$

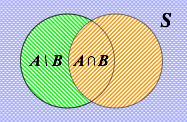
例如，在由一共 32 張牌構成的斯卡特撲克牌中隨機抽出一張，其或者是"方片"或者是"${\displaystyle {\mathcal {A}}}$"的機率是多少？

事件 ${\displaystyle A}$，${\displaystyle B}$ 是或者的關係，且可同時發生，就是說抽出的這張牌即可以是"方片"，又可以是"${\displaystyle {\mathcal {A}}}$"，${\displaystyle A}$ ∩ ${\displaystyle B}$ ( 既發生 ${\displaystyle A}$又發生 ${\displaystyle B}$ ) 的值是 1 / 32，( 從示意圖上也可以看出，即是方片又是${\displaystyle {\mathcal {A}}}$只有一張，即機率是 1 / 32 )，因此有如下結果：
${\displaystyle P(A\cup B)={\frac {8}{32}}+{\frac {4}{32}}-{\frac {1}{32}}={\frac {11}{32}}}$

注意到公理 3 是定理 5 的特殊情況，即 ${\displaystyle A}$，${\displaystyle B}$ 不同時發生，相應的 P(A∩B)=0。

定理 6 (乘法法則)[編輯]

輪盤遊戲示意圖 2

事件 ${\displaystyle A}$，${\displaystyle B}$ 同時發生的機率是：

${\displaystyle P(A\cap B)=P(A)\cdot P(B\vert A)=P(B)\cdot P(A\vert B)}$

公式中的 ${\displaystyle P(A|B)}$ 是指在 ${\displaystyle B}$ 條件下 ${\displaystyle A}$ 發生的機率，又稱作條件機率。回到上面的斯卡特遊戲中，在 32 張牌中隨機抽出一張，即是方片又是${\displaystyle {\mathcal {A}}}$的機率是多少呢？現用${\displaystyle P(A)}$ 代表抽出方片的機率，用 ${\displaystyle P(B)}$ 代表抽出${\displaystyle {\mathcal {A}}}$的機率，很明顯，${\displaystyle A}$，${\displaystyle B}$ 之間有一定聯繫，即 ${\displaystyle A}$ 里包含有 ${\displaystyle B}$，${\displaystyle B}$ 里又包含有 ${\displaystyle A}$，在 ${\displaystyle A}$ 的條件下發生 ${\displaystyle B}$ 的機率是 P(B | A)=1/8，則有：

${\displaystyle P(A\cap B)=P(A)\cdot P(B\vert A)={\frac {8}{32}}\cdot {\frac {1}{8}}={\frac {1}{32}}}$

或者，${\displaystyle P(A\cap B)=P(B)\cdot P(A\vert B)={\frac {4}{32}}\cdot {\frac {1}{4}}={\frac {1}{32}}}$
從上面的圖中也可以看出，符合條件的只有一張牌，即方片${\displaystyle {\mathcal {A}}}$。

另一個例子，在 32 張斯卡特牌里連續抽兩張 ( 第一次抽出的牌不放回去 )，連續得到兩個${\displaystyle {\mathcal {A}}}$的機率是多少呢？
設 ${\displaystyle A}$，${\displaystyle B}$ 分別為連續發生的這兩次事件，我們看到，${\displaystyle A}$，${\displaystyle B}$ 之間有一定聯繫，即 ${\displaystyle B}$ 的機率由於 ${\displaystyle A}$ 發生了變化，屬於條件機率，按照公式有：${\displaystyle P(A\cap B)=P(A)\cdot P(B\vert A)={\frac {4}{32}}\cdot {\frac {3}{31}}={\frac {3}{248}}}$

定理 7 (無關事件乘法法則)[編輯]

兩個不相關聯的事件 ${\displaystyle A}$，${\displaystyle B}$ 同時發生的機率是：

${\displaystyle P(A\cap B)=P(A)\cdot P(B)}$

注意到這個定理實際上是定理 6 (乘法法則) 的特殊情況，如果事件 ${\displaystyle A}$，${\displaystyle B}$ 沒有聯繫，則有 P(A|B)=P(A)，以及 P(B|A)=P(B)。現在觀察一下輪盤遊戲中兩次連續的旋轉過程，${\displaystyle P(A)}$ 代表第一次出現紅色的機率，${\displaystyle P(B)}$ 代表第二次出現紅色的機率，可以看出，${\displaystyle A}$ 與 ${\displaystyle B}$ 沒有關聯，利用上面提到的公式，連續兩次出現紅色的機率為：

${\displaystyle P(A\cap B)={\frac {18}{37}}\cdot {\frac {18}{37}}=0.2367}$

忽視這一定理是造成許多玩家失敗的根源，普遍認為，經過連續出現若干次紅色後，黑色出現的機率會越來越大，事實上兩種顏色每次出現的機率是相等的，之前出現的紅色與之後出現的黑色之間沒有任何聯繫，因為球本身並沒有「記憶」，它並不「知道」以前都發生了什麼。同理，連續 10 次出現紅色的機率為 P=(18/37)¹⁰ =0.0007

完全機率[編輯]

${\displaystyle n}$ 個事件 ${\displaystyle H_{1},H_{2},...H_{n}}$ 互相間獨立，且共同組成整個事件空間 ${\displaystyle S}$，即
${\displaystyle H_{i}\cap H_{j}=\varnothing }$，${\displaystyle (i\neq j)}$ 以及
${\displaystyle H_{1}\cup H_{2}\cup ...\cup H_{n}=S}$
這時 ${\displaystyle A}$ 的機率可以表示為，

${\displaystyle P(A)=\sum _{j=1}^{n}P(A|H_{j})\cdot P(H_{j})}$

證明：

${\displaystyle A=(A\cap H_{1})\cup (A\cap H_{2})\cup \ldots \cup (A\cap H_{n})}$
按照公理 3 ，有
${\displaystyle P(A)=P(A\cap H_{1})+P(A\cap H_{2})+\ldots +P(A\cap H_{n})}$
根據乘法法則，${\displaystyle P(A\cap H_{j})=P(A|H_{j})\cdot P(H_{j})}$
因此有，
${\displaystyle P(A)=P(A|H_{1})\cdot P(H_{1})+\ldots +P(A|H_{n})\cdot P(H_{n})}$
${\displaystyle P(A)=\sum _{j=1}^{n}P(A|H_{j})\cdot P(H_{j})}$

例如，一個隨機試驗工具由一個骰子和一個柜子中的三個抽屜組成，抽屜 1 里有 14 個白球和 6 個黑球，抽屜 2 里有 2 個白球和 8 個黑球，抽屜 3 里有 3 個白球和 7 個黑球，試驗規則是首先擲骰子，如果獲得小於 4 點，則抽屜 1 被選擇，如果獲得 4 點或者 5 點，則抽屜 2 被選擇，其他情況選擇抽屜 3 。然後在選擇的抽屜里隨機抽出一個球，最後抽出的這個球是白球的機率是：

P(白)=P(白|抽1)·P(抽1)+P(白|抽2)·P(抽2)＋P(白|抽3)·P(抽3)

=(14/20)·(3/6)+(2/10)·(2/6)+(3/10)·(1/6)

=28/60=0.4667

從例子中可看出，完全機率特別適合於分析具有多層結構的隨機試驗的情況。

貝葉斯定理[編輯]

主條目：貝葉斯定理

貝葉斯定理由英國數學家托馬斯·貝葉斯 ( Thomas Bayes 1702-1761 ) 發展，用來描述兩個條件機率之間的關係，比如 P(A|B) 和 P(B|A)。按照定理 6 的乘法法則，P(A∩B)=P(A)·P(B|A)=P(B)·P(A|B)，可以立刻導出貝葉斯定理：

${\displaystyle P(A\vert B)={\frac {P(B\vert A)\cdot P(A)}{P(B)}}}$

例如：一座別墅在過去的 20 年裡一共發生過 2 次被盜，別墅的主人有一條狗，狗平均每周晚上叫 3 次，在盜賊入侵時狗叫的機率被估計為 0.9，問題是：在狗叫的時候發生入侵的機率是多少？
我們假設 ${\displaystyle A}$ 事件為狗在晚上叫，${\displaystyle B}$ 為盜賊入侵，則 ${\displaystyle P(A)=3/7}$，${\displaystyle P(B)}$=2/(20·365.25)=2/7305，P(A | B) = 0.9，按照公式很容易得出結果：
${\displaystyle P(B\vert A)=0.9\cdot {\frac {2}{7305}}\cdot {\frac {7}{3}}=0.0005749486653...}$

另一個例子，現分別有 ${\displaystyle A}$，${\displaystyle B}$ 兩個容器，在容器 ${\displaystyle A}$ 里分別有 7 個紅球和 3 個白球，在容器 ${\displaystyle B}$ 里有 1 個紅球和 9 個白球，現已知從這兩個容器里任意抽出了一個球，且是紅球，問這個紅球是來自容器 ${\displaystyle A}$ 的機率是多少?

假設已經抽出紅球為事件 ${\displaystyle B}$，從容器 ${\displaystyle A}$ 里抽出球為事件 ${\displaystyle A}$，則有：${\displaystyle P(B)}$ = 8 / 20，${\displaystyle P(A)}$ = 1 / 2，${\displaystyle P(B|A)}$ = 7 / 10，按照公式，則有：
${\displaystyle P(A\vert B)={\frac {7}{10}}\cdot {\frac {1}{2}}\cdot {\frac {20}{8}}={\frac {7}{8}}}$